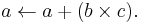Multiply–accumulate operation

In computing, especially digital signal processing, the multiply–accumulate operation is a common step that computes the product of two numbers and adds that product to an accumulator. The hardware unit that performs the operation is known as a multiplier–accumulator (MAC, or MAC unit); the operation itself is also often called a MAC or a MAC operation. The MAC operation modifies an accumulator a:

When done with floating point numbers, it might be performed with two roundings (typical in many DSPs), or with a single rounding. When performed with a single rounding, it is called a fused multiply–add (FMA) or fused multiply–accumulate (FMAC).

Modern computers may contain a dedicated MAC, consisting of a multiplier implemented in combinational logic followed by an adder and an accumulator register that stores the result. The output of the register is fed back to one input of the adder, so that on each clock cycle, the output of the multiplier is added to the register. Combinational multipliers require a large amount of logic, but can compute a product much more quickly than the method of shifting and adding typical of earlier computers. The first processors to be equipped with MAC units were digital signal processors, but the technique is now also common in general-purpose processors.

In floating-point arithmetic

When done with integers, the operation is typically exact (computed modulo some power of 2). However, floating-point numbers have only a certain amount of mathematical precision. That is, digital floating-point arithmetic is generally not associative or distributive. (See Floating point#Accuracy problems.) Therefore, it makes a difference to the result whether the multiply–add is performed with two roundings, or in one operation with a single rounding (a fused multiply–add).

Fused multiply–add

A fused multiply–add is a floating-point multiply–add operation performed in one step, with a single rounding. That is, where an unfused multiply–add would compute the product b×c, round it to N significant bits, add the result to a, and round back to N significant bits, a fused multiply–add would compute the entire sum a+b×c to its full precision before rounding the final result down to N significant bits.

A fast FMA can speed up and improve the accuracy of many computations that involve the accumulation of products:

• Dot product
• Matrix multiplication
• Polynomial evaluation (e.g., with Horner's rule)
• Newton's method for evaluating functions.

Fused multiply–add can usually be relied on to give more accurate results. However, Kahan has pointed out that it can give problems if used unthinkingly.^[1] If x² − y² is evaluated as ((x×x) − y×y) using fused multiply–add, then the result may be negative even when x = y due to the first multiplication discarding low significance bits. This could then lead to an error if for instance the square root of the result is then evaluated.

When implemented inside a microprocessor, an FMA can actually be faster than a multiply operation followed by an add, even though standard industrial implementations based on the original IBM RS/6000 design require a 2N-bit adder to compute the sum properly.^[2][3]

A useful benefit of including this instruction is that it allows an efficient software implementation of division and square root operations, thus eliminating the need for dedicated hardware for those operations.^[4]

The FMA operation is included in IEEE 754-2008.

The DEC VAX's POLY instruction is used for evaluating polynomials with Horner's rule using a succession of fused multiply–add steps.^[5] This instruction has been a part of the VAX instruction set since its original 11/780 implementation in 1977.

The 1999 standard of the C programming language supports the FMA operation through the fma standard math library function.

The fused multiply–add operation was introduced as multiply–add fused in the IBM POWER1 processor,^[6] but has been added to numerous other processors since then:

• Fujitsu SPARC64 VI (2007) and above
• HP PA-8000 (1996) and above
• SCE-Toshiba Emotion Engine (1999)
• Intel Itanium (2001)
• STI Cell (2006)
• (MIPS-compatible) Loongson-2F (2008).^[7]
• ARM with VFPv4 (which is optional) ^[8]

An FMA instruction will be implemented in the newer AMD CPUs like 'Bulldozer' with FMA4 support. Intel plans to implement FMA3 in processors using its Haswell microarchitecture, due in late 2012.^[9]

FMA capability is also present in the NVIDIA GeForce 200 Series (GTX 200) GPUs, GeForce 400 Series, GeForce 500 Series GPUs and the NVIDIA Tesla C1060 Computing Processor & C2050 / C2070 GPU Computing Processor GPGPUs.^[10] FMA has been added to the AMD Radeon line with the HD 5000 series.^[11]

References